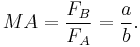Lever

Lever

Levers can be used to exert a large force over a small distance at one end by exerting only a small force over a greater distance at the other.
Classification Simple machine
Industry Construction

A lever is constructed from a beam attached to ground by a hinge, or fulcrum. It is one of the six simple machines identified by Renaissance scientists. The word comes from the French lever, "to raise", cf. a levant. A lever amplifies an input force to provide a greater output force, which is said to provide leverage. The ratio of the output force to the input force is the mechanical advantage of the lever.

Contents

Early use

The earliest remaining writings regarding levers date from the 3rd century BC and were provided by Archimedes. "Give me a place to stand, and I shall move the Earth with a lever"[note 1] is a remark of Archimedes who formally stated the correct mathematical principle of levers (quoted by Pappus of Alexandria).[1]

It is assumed that in ancient Egypt, constructors used the lever to move and uplift obelisks weighting more than 100 tons.[2]

Force and levers

A lever is a beam connected to ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces. This is known as the law of the lever.

Mathematically, this is expressed by 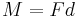M = F d, where F is the force, d is the perpendicular distance between the force and the fulcrum, and M is the turning force known as the moment or torque.

Classes of levers

Levers are classified by the relative positions of the fulcrum and the input and output forces. It is common to call the input force the effort and the output force the load or the resistance. This allows the identification of three classes of levers by the relative locations of the fulcrum, the resistance and the effort:[3]

These cases are described by the mnemonic "fre 123" where the fulcrum is in the middle for the 1st class lever, the resistance is in the middle for the 2nd class lever, and the effort is in the middle for the 3rd class lever.

Law of the lever

The lever is a movable bar that pivots on a fulcrum attached to a fixed point. The lever operates by applying forces at different distances from the fulcrum, or pivot.

Assuming the lever does not dissipate or store energy, the power into the lever must equal the power out of the lever. As the lever rotates around the fulcrum, points farther from this pivot move faster than points closer to the pivot. Therefore a force applied to a point farther from the pivot must be less than the force located at a point closer in, because power is the product of force and velocity.[4]

If a and b are distances from the fulcrum to points A and B and let the force FA applied to A is the input and the force FB applied at B is the output, the ratio of the velocities of points A and B is given by a/b, so we have the ratio of the output force to the input force, or mechanical advantage, is given by

MA = \frac{F_B}{F_A} = \frac{a}{b}.

This is the law of the lever, which was proven by Archimedes using geometric reasoning.[5] It shows that if the distance a from the fulcrum to where the input force is applied (point A) is greater than the distance b from fulcrum to where the output force is applied (point B), then the lever amplifies the input force. On the other hand, if the distance a from the fulcrum to the input force is less than the distance b from the fulcrum to the output force, then the lever reduces the input force.

The use of velocity in the static analysis of a lever is an application of the principle of virtual work.

See also

Notes

  1. ^ If this feat were attempted in a uniform gravitational field with an acceleration equivalent to that of the Earth, the corresponding distance to the fulcrum which a human of mass 70kg would be required to stand to balance a sphere of 1 Earth mass, with center of gravity 1m to the fulcrum, would be roughly equal to 8.5×1022m. This distance might be exemplified in astronomical terms as the approximate distance to the Circinus galaxy (roughly 3.6 times the distance to the Andromeda Galaxy).

References

  1. ^ Mackay, Alan Lindsay (1991). "Archimedes ca 287–212 BC". A Dictionary of scientific quotations. London: Taylor and Francis. p. 11. ISBN 9780750301060. 
  2. ^ Budge, E.A. Wallis (2003). Cleopatra's Needles and Other Egyptian Obelisks‎. Kessinger Publishing. p. 28. ISBN 9780766135246. 
  3. ^ Davidovits, Paul (2008), Physics in Biology and Medicine, Third edition, Academic Press, p. 10, ISBN 978-0-12-369411-9, http://books.google.be/books?id=e9hbt3xisb0C , Chapter 1, p. 10
  4. ^ Uicker, John; Pennock, Gordon; Shigley, Joseph (2010). Theory of Machines and Mechanisms (4th ed.). Oxford University Press, USA. ISBN 978-0195371239. 
  5. ^ Usher, Abbott (1988). A history of mechanical inventions (revised, illustrated ed.). Courier Dover Publications. pp. 94. ISBN 9780486255934. 

External links

Classical simple machines
Inclined plane · Lever · Pulley · Screw · Wedge · Wheel and axle